When I was a child, I remember staring up at the night sky, filled with countless stars, wondering about the mysteries of the universe. Little did I know that centuries ago, a man named Sir Isaac Newton had gazed upon the same sky and unlocked secrets that would change our understanding of the world forever. His story isn't just about laws of physics; it's about curiosity, perseverance, and a relentless quest for knowledge that continues to inspire us today.
Introduction
Newton's Achievements
How Did Newton Solve Problems?
Newton's Method of Research
Conclusion
The Early Life of a Curious Mind
Born on a chilly Christmas Day in 1642, in the tiny hamlet of Woolsthorpe, England, Isaac Newton's entrance into the world was as humble as it gets. His father had passed away before his birth, and his mother remarried and left young Isaac in the care of his grandmother. Growing up, he wasn't the most sociable child, often preferring solitary activities over playing with peers. Yet, this solitude may have been the fertile ground where his inquisitive mind began to flourish.
I recall reading a biography of Newton during my college years, and I was struck by how his early experiences seemed to shape his future endeavors. Just like many of us who find solace in books and learning, Newton immersed himself in his studies, perhaps as a way to make sense of the world around him.
A Fruit That Sparked a Revelation
We all know the famous story: Newton sitting under an apple tree, an apple falls, and suddenly, the law of gravity is born. While this tale might be more legend than fact, it encapsulates how Newton's observations of everyday phenomena led to groundbreaking theories. Imagine watching an apple fall and contemplating not just why it falls, but how that same force affects the moon and the stars. It's this leap from the ordinary to the extraordinary that defines Newton's genius.
Newton's Law of Universal Gravitation
Newton's law of universal gravitation wasn't just about apples and trees; it was a mathematical description of a force that affects every object in the universe. He proposed that every mass attracts every other mass with a force proportional to the product of their masses and inversely proportional to the square of the distance between their centers. This was revolutionary! It unified the celestial and the terrestrial, showing that the same laws governed both the heavens and the earth.
When I pondered this concept in my physics class, it was mind-blowing to realize how one individual could connect such vast ideas. It made me appreciate the beauty of theoretical reasoning combined with empirical evidence.
Unlock your inner Newton, and you will find the answers to life's most significant problems.
The Principia Mathematica
In 1687, Newton published the Philosophiæ Naturalis Principia Mathematica, commonly known as the Principia. This work is often regarded as one of the most important in the history of science. In it, Newton laid out his three laws of motion and universal gravitation, which became the foundation for classical mechanics.
I once tried to read passages from the Principia, and while the archaic language was challenging, the concepts were brilliant. Newton didn't just present theories; he provided mathematical proofs and experiments to back them up. It's a testament to how meticulous and thorough his research methods were.
Exploring the Nature of Light and Color
Newton wasn't content with just mechanics; he delved into optics, studying the nature of light and color. Through experiments, he demonstrated that white light is composed of a spectrum of colors, which can be seen when passed through a prism. This discovery challenged the existing notions of the time.
I remember conducting a similar experiment in high school, using a prism to split light into a rainbow. That simple act connected me to Newton's work centuries earlier. It was fascinating to physically see the spectrum and understand the underlying principles.
The Birth of Calculus
One of Newton's lesser-known, yet equally significant achievements was the development of calculus. Around the same time, German mathematician Gottfried Wilhelm Leibniz was also working on calculus, leading to one of the most famous disputes in mathematical history over who discovered it first.
Calculus, the mathematical study of continuous change, is essential in fields like physics, engineering, and economics. Newton used it to formulate his laws and analyze motion and change. Personally, when I struggled through calculus classes, knowing that Newton had a hand in its creation added a layer of historical appreciation.
How Did Newton Solve Problems?
Newton's approach to problem-solving was nothing short of remarkable. He possessed an uncanny ability to observe, hypothesize, experiment, and conclude. His methods combined the empirical with the theoretical, bridging gaps that others couldn't.
A Blend of Empiricism and Rationalism
Newton didn't rely solely on observation or abstract reasoning; he used both in harmony. For instance, when examining the motion of planets, he didn't just accept existing models. He observed astronomical data, applied mathematical calculations, and formulated theories that aligned with both the observations and logical principles.
This approach reminds me of how we tackle complex issues today. Whether we're dealing with scientific research or even drafting a reassignment request letter with tips and information, combining practical evidence with sound reasoning leads to the best outcomes.
Persistence and Patience
Newton was known for his intense focus. He could spend hours, days, or even months on a single problem. One story tells of how he would get so engrossed in his work that he forgot to eat or sleep. His ability to concentrate deeply on a subject is something that many of us can aspire to, especially in an age of constant distractions.
I often find myself struggling to maintain that level of focus, but thinking about Newton's dedication inspires me to try harder. It's a reminder that great achievements often require great perseverance.
Newton's Method of Research
Intense Study and Experimentation
Newton was notorious for his rigorous study habits. He wasn't afraid to "mangle" his books, scribbling notes in the margins, underlining passages, and engaging actively with the material. This kind of interaction with texts shows a deep engagement with learning.
In college, I adopted a similar approach, highlighting and annotating my textbooks. It made the learning process more interactive and helped me retain information better.
Embracing Mistakes as Learning Opportunities
Newton didn't shy away from making mistakes. In fact, he saw them as stepping stones to greater understanding. He would test hypotheses, and if they didn't hold up, he would adjust and try again. This iterative process is the essence of the scientific method.
In our own lives, whether we're conducting research or navigating personal challenges, adopting Newton's mindset can be incredibly beneficial. It's okay to err; what's important is that we learn and keep moving forward.
Understanding Newton's Laws of Motion
Newton's three laws of motion form the basis of classical mechanics. They describe the relationship between a body and the forces acting upon it, and its motion in response to those forces.
1- First Law (Law of Inertia): An object will remain at rest or in uniform motion in a straight line unless acted upon by an external force.
This law challenges us to think about how inertia affects our daily lives. For instance, when we're in a car that suddenly stops, we feel a jolt forward due to our body's inertia.
2- Second Law (F=ma): The acceleration of an object is dependent upon the net force acting upon it and inversely proportional to its mass.
This explains why pushing a heavy object requires more effort than pushing a lighter one.
3- Third Law (Action and Reaction): For every action, there is an equal and opposite reaction.
This is observable when we jump off a small boat onto a dock, and the boat moves backward.
By understanding these laws, we gain insight into the fundamental principles that govern motion. It's fascinating to see how these principles apply to everything from launching rockets to playing sports.
The Impact of Newton's Discoveries on Modern Science
Foundations for Future Scientists
Newton's work laid the groundwork for countless scientific advancements. His laws of motion and universal gravitation were pivotal for later scientists like Albert Einstein, who developed the theory of relativity, expanding upon Newtonian physics.
I find it fascinating how knowledge builds upon itself. Each generation of scientists stands on the shoulders of giants, pushing the boundaries further. It's a continuous journey of discovery.
Influence Beyond Science
Newton's methodologies have influenced not just science but also the way we approach problems in other fields. His insistence on empirical evidence and logical reasoning is mirrored in disciplines ranging from philosophy to economics.
When I'm faced with complex decisions at work, I often think about how data-driven analysis can lead to better outcomes. It's about gathering information, weighing options logically, and making informed choices.
Lessons We Can Learn from Newton
The Power of Curiosity
Newton's insatiable curiosity drove him to ask questions that others hadn't considered. This trait is invaluable in any field. By fostering curiosity in ourselves and others, we open doors to new ideas and innovations.
Dedication to Lifelong Learning
Even after achieving significant success, Newton never stopped learning. He continued to explore new areas, write, and engage with the scientific community. Lifelong learning keeps the mind sharp and the spirit youthful.
I try to emulate this by reading widely, attending workshops, and staying open to new experiences. It's amazing how much there is to discover if we keep an open mind.
Balancing Theory and Practice
Newton's work exemplifies the balance between theoretical knowledge and practical application. Whether in science, business, or personal endeavors, finding this balance can lead to more effective solutions.
Embracing Newton's Approach in Our Lives
While we might not all be scientific geniuses, we can apply Newton's principles in our own lives:
Be Observant: Pay attention to the world around us. Sometimes, the simplest observations can lead to profound insights.
Be Persistent: Challenges are inevitable. Persisting through difficulties often leads to breakthroughs.
Be Analytical: Use logical reasoning to solve problems. Break down complex issues into manageable parts.
Be Open to New Ideas: Don't be afraid to challenge existing beliefs. Innovation often comes from thinking differently.
Continue Learning: Embrace lifelong learning to keep growing personally and professionally.
A Personal Reflection on Newton's Influence Today
I can't help but think about how Newton's methodologies can be applied in our modern world. Take, for example, the way we handle project management in businesses. Newton's emphasis on careful observation and analysis can improve how we plan and execute tasks.
Applying Newtonian Principles in the Workplace
When tasked with leading a new project, I decided to observe the current processes in place. By gathering data and understanding the dynamics, I could develop a plan grounded in reality. Then, I used rational analysis to address potential obstacles, much like Newton might have when formulating his theories.
I also encouraged my team to adopt a scientific approach:
1- Identify the Problem: Clearly define what we're trying to solve.
2- Gather Information: Collect relevant data and insights.
3- Formulate Hypotheses: Brainstorm potential solutions.
4- Test Solutions: Implement ideas on a small scale to see what works.
5- Analyze Results: Assess outcomes and refine as needed.
This method led to more efficient workflows and improved team morale. It's amazing how principles from centuries ago can still be relevant!
Embracing Continuous Improvement
Newton's dedication to lifelong learning inspires me to keep pushing myself. Whether it's picking up a new hobby or delving into professional development courses, the pursuit of knowledge enriches life.
I recently took up coding, despite having no background in it. The process of learning a new language, debugging code, and seeing the results come to life is rewarding. It reminds me of how Newton must have felt when his experiments led to new discoveries.
The Human Side of Newton
While we often focus on Newton's intellectual achievements, it's important to remember that he was human too. He faced challenges, had disagreements (like his feud with Leibniz over calculus), and struggled with personal issues.
Overcoming Adversity
Newton lived through the Great Plague of London in 1665, which led him to return to his family home. It was during this time, often referred to as his "year of wonders," that he made some of his most significant discoveries. This period shows how adversity can sometimes lead to unexpected opportunities.
In our current times, dealing with global challenges, we can take comfort in knowing that difficult periods can also be times of growth and innovation.
Personal Relationships and Solitude
Newton was known to be a private person, often preferring solitude. Some speculate that this allowed him to focus intensely on his work. However, he also engaged with the Royal Society and corresponded with other thinkers of his time.
This balance between introspection and collaboration is something we can learn from. While deep work requires focus, sharing ideas with others can enhance understanding and lead to new insights.
Conclusion
Sir Isaac Newton's legacy is not just in the monumental scientific discoveries he made, but also in the way he approached problems and conducted his research. His blend of curiosity, persistence, and rigorous methodology serves as an enduring example for us all.
As I reflect on Newton's life, I realize that his contributions extend beyond science. They touch on fundamental aspects of human endeavor: the quest for knowledge, the courage to challenge the unknown, and the dedication to pursue one's passions relentlessly.
Unlocking our inner Newton isn't about becoming the next great physicist; it's about embracing the qualities that lead to personal and collective growth. By cultivating curiosity, embracing challenges, and applying thoughtful analysis, we too can make meaningful contributions to our world.
References
1- Gleick, James. Isaac Newton. New York: Vintage Books, 2004.
2- Westfall, Richard S. Never at Rest: A Biography of Isaac Newton. Cambridge: Cambridge University Press, 1980.
3- Newton, Isaac. Philosophiæ Naturalis Principia Mathematica. London: Joseph Streater, 1687.
4- Cohen, I. Bernard, and George E. Smith. The Cambridge Companion to Newton. Cambridge: Cambridge University Press, 2002.
5- Aiton, E. J. The Vortex Theory of Planetary Motions. London: MacDonald, 1972.
Frequently Asked Questions
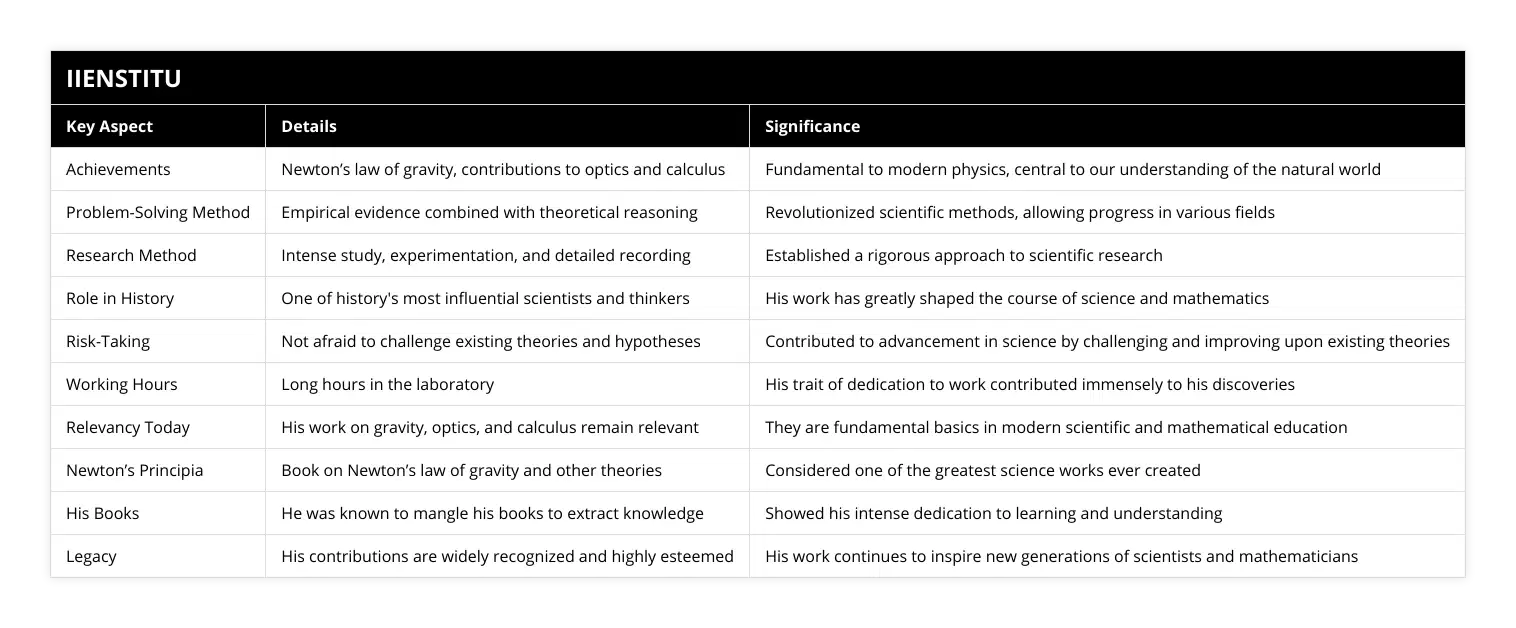
What achievements did Newton make in problem solving?
Sir Isaac Newton (1642-1727) is regarded as one of the most outstanding scientists. He made groundbreaking advances in mathematics, optics, physics, and astronomy. He is particularly noted for his contribution to the field of problem-solving. In this article, we will explore some of Newton’s most significant achievements in problem-solving.
One of Newton’s most notable contributions to problem-solving was his development of calculus. Calculus is a powerful tool used to solve various mathematical problems. Newton developed the fundamental principles of calculus in the late 1600s, and it has since become a cornerstone of mathematics. His work on calculus revolutionized the way mathematicians approach and solve problems.
Newton also developed several effective methods for solving equations. His “Newton’s Method” is a widely used technique for finding the roots of equations. His “Fluxion Method” is a technique used to solve differential equations. Both of these methods are widely used today in engineering and physics.
Newton was also a pioneer in the field of optics. He developed the first reflecting telescope and explained the laws of refraction and reflection. His work in optics laid the foundation for developing modern optical instruments, such as microscopes and telescopes.
Finally, Newton made groundbreaking contributions to the field of astronomy. He developed a theory of gravity, which explained the motion of planets and other celestial bodies. His work led to the discovery of the law of universal gravitation, which states that every object in the universe is attracted to every other thing. This law laid the foundation for modern physics and astronomy.
In summary, Newton made several remarkable contributions to problem-solving. He developed calculus, a powerful mathematical tool, and several effective methods for solving equations. He also made groundbreaking discoveries in optics and astronomy. His work laid the foundation for modern physics and astronomy, shaping our understanding of the universe.
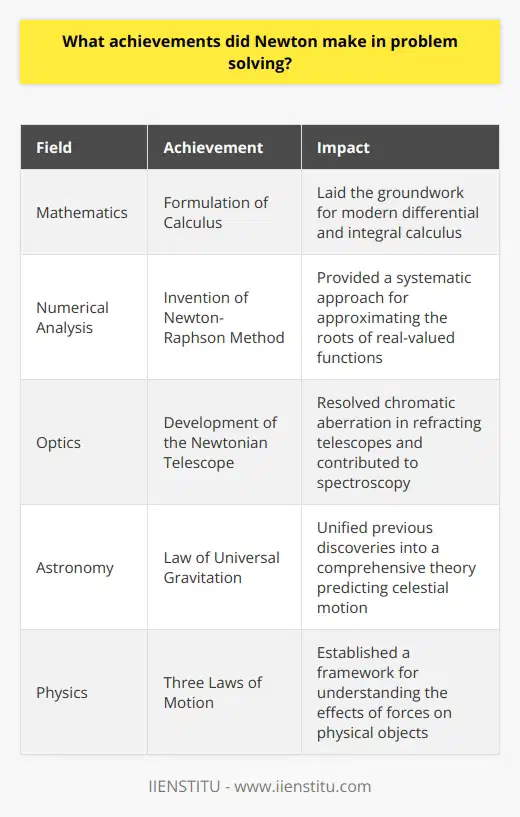
How did Newton approach problem solving?
Sir Isaac Newton is widely regarded as one of the most influential scientists. He was a mathematician, physicist, and astronomer who made groundbreaking advances in mathematics, optics, and gravity. He is perhaps most famously known for his development of the laws of motion and the law of universal gravitation. But how did he go about problem-solving?
Newton was a meticulous thinker who did not take shortcuts in his work. He believed problems should be addressed with a systematic and logical observation, experimentation, and analysis approach. He was a master analyst, able to break down complex problems into their parts and analyze them separately. He would then reconstruct the evidence to formulate a solution. His approach to problem-solving was based on a combination of inductive and deductive reasoning.
Newton was also a believer in the empirical approach, meaning that he would base his conclusions on observation and experimentation. This was particularly evident in his development of the law of gravity, which he formulated after observing the motion of the planets. He also used mathematical models to simulate the behavior of complex systems, such as the motion of the planets.
Newton was also unafraid to challenge accepted ideas and theories. He was known for his willingness to question the assumptions of others and his own beliefs. This allowed him to develop new insights into existing problems.
In summary, Newton's approach to problem-solving was based on careful analysis, observation, and experimentation. He was unafraid to challenge existing assumptions and beliefs and was willing to use mathematics to simulate complex systems. His approach has since become the foundation of the scientific method, and his insights continue to influence modern science.
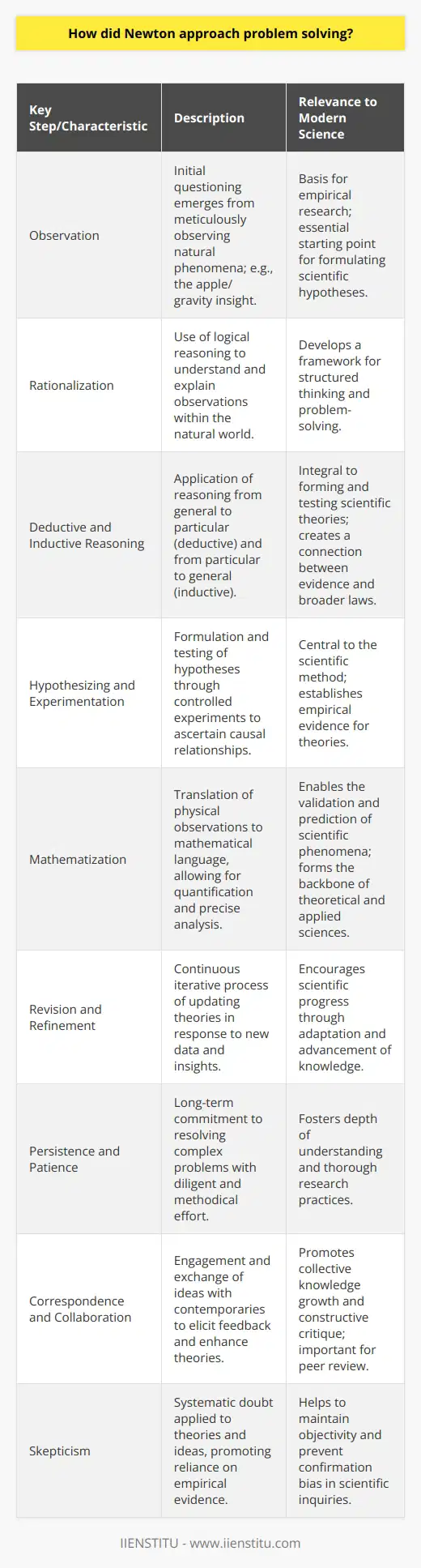
What is the significance of Newton's method of research?
Sir Isaac Newton's research method has been of great significance in developing scientific knowledge throughout history. His approach to scientific inquiry was the first of its kind, incorporating mathematics and observation to create a unified theory of the physical world. Newton's research method was particularly revolutionary in that it was based on inductive reasoning, which is the process of deriving general principles from specific observations. This approach allowed him to connect previously unrelated phenomena, opening up a new way of looking at the universe.
Newton's research method was significant because it established the groundwork for modern scientific inquiry. His emphasis on using mathematics to explain physical phenomena was a considerable step forward in developing scientific knowledge. Furthermore, his use of experimentation and observation to support his theories was a substantial departure from the Aristotelian approach of relying solely on philosophical reasoning. This shift in methodology led to a much more rigorous and reliable form of scientific inquiry, which was instrumental in advancing our understanding of the natural world.
Perhaps the essential contribution of Newton's research method was the development of the scientific method. His approach of combining mathematics, experimentation, and observation provided a framework for subsequent generations of scientists to build upon. His work has since served as a foundation for many of the great discoveries of modern science, including the theories of relativity, quantum mechanics, and genetics.
In conclusion, Newton's research method has been of great significance in developing scientific knowledge throughout history. His revolutionary approach of combining mathematics, experimentation, and observation provided the groundwork for modern scientific inquiry and has since served as a foundation for many of the great discoveries of modern science. Moreover, his work continues to be an invaluable inspiration for future scientists.

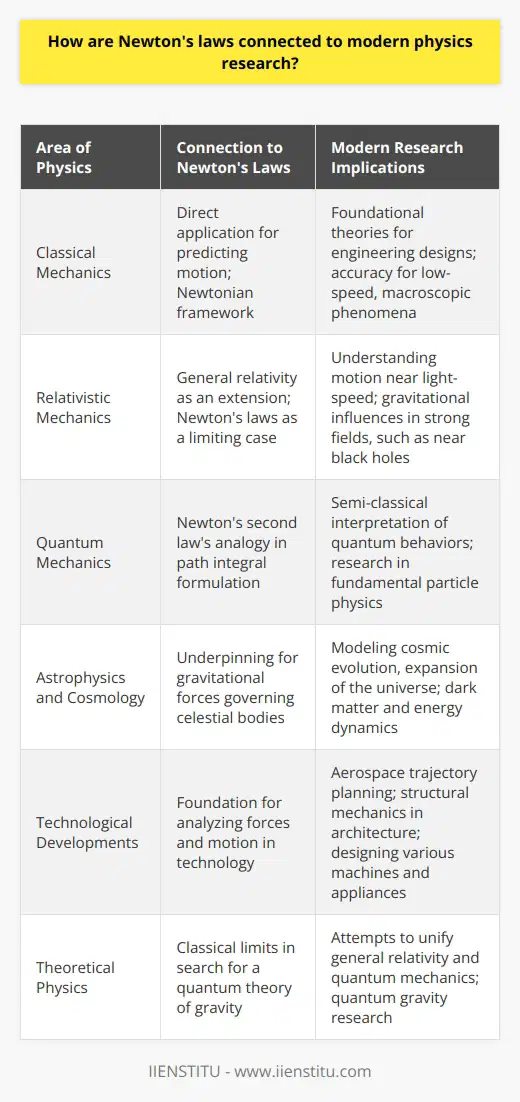
How can I improve my physics problem-solving skills?
Develop a Strong Foundation
Improving physics problem-solving skills begins with building a strong foundation in both theoretical knowledge and mathematical techniques. To do this, focus on mastering core concepts, actively participating in classroom discussions, and engaging in individual or group study sessions. Dedicate time to reviewing textbooks and supplementary materials, as well as engaging with online resources, such as video lectures, simulations, and podcasts.
Practice Regularly
Consistent practice is essential for developing problem-solving abilities. Allocate time to work on physics problems from various sources like textbooks, online platforms, and question banks on a daily basis. To maximize efficiency, focus on understanding the given problems, identifying the relevant principles and equations involved, and formulating an appropriate strategy before diving into calculations. Consider working through alternative solution methods to broaden your understanding of concepts and enhance adaptability.
Build an Intuitive Understanding
Deepening your understanding of physics concepts requires developing intuition about their real-world applications. A clear mental visualization of the physical phenomena under consideration can streamline problem-solving and facilitate a more profound appreciation of the topic. Relax and think calmly, imagining the scenario presented in the problem statement. Attempt to draw diagrams, schematics or even doodles to help create a clearer mental image. This approach can be particularly helpful when tackling challenging or unfamiliar problems.
Collaborate with Peers
Working together with classmates or study partners can significantly improve problem-solving skills. Collaborative discussions encourage the exchange of ideas, provide exposure to different perspectives, and facilitate the identification of common misunderstandings. Sharing individual problem-solving strategies can help to recognize personal strengths and weaknesses, ultimately leading to more efficient learning.
Learn from Mistakes
Mistakes and misconceptions are inevitable when learning physics; however, they can provide valuable learning opportunities. Embrace mistakes and strive to understand why they occurred. Analyze errors made during problem-solving exercises, identify their root causes, and work to correct misunderstandings. Regularly engaging in such self-assessment can contribute to the gradual refinement of problem-solving techniques and overall improvement in physics competency.
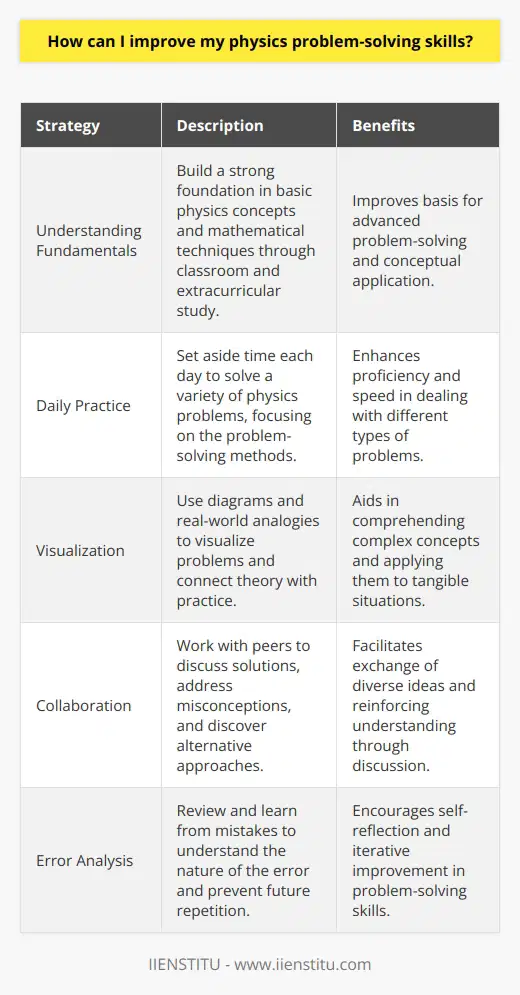
What are the 3 steps for solving a problem in physics?
Identifying the Problem
The first essential step in solving a problem in physics is to identify the problem's specific aspects. This involves understanding the scenario, determining the variables and conditions involved, and figuring out the appropriate physics concepts to apply. Grasping the problem statement's essential information allows one to establish a clear mental picture of the situation at hand. Moreover, it helps in distinguishing any missing or extra data provided and simplifies the process of problem-solving.
Creating a Strategy
Once the problem is identified and the relevant information is extracted, the next step involves creating a systematic strategy to solve the problem. This typically includes deciding the approach, breaking the problem into smaller parts, setting up equations, and selecting the best method for solving them. It is crucial at this stage to review the applicable laws, principles, and formulas that govern the particular physics concepts being explored. In case of more complex problems, remember to consider multiple approaches to find the most appropriate path towards the solution. Developing a strategy streamlines the process and ensures accuracy in the final answer.
Executing the Solution
With a thorough understanding of the problem and a well-crafted strategy, one can now proceed to execute the solution. This usually entails substituting the given variables in equations, performing mathematical calculations, and evaluating the outcome. While doing so, maintain vigilance in unit management and conversion factors, as well as error minimization and proper rounding. If necessary, iterate the calculations using different techniques to ensure correctness. The final solution should be accompanied by a qualitative check, ensuring that the resulting values and relationships align with the original problem statement and are logically consistent with physical principles.
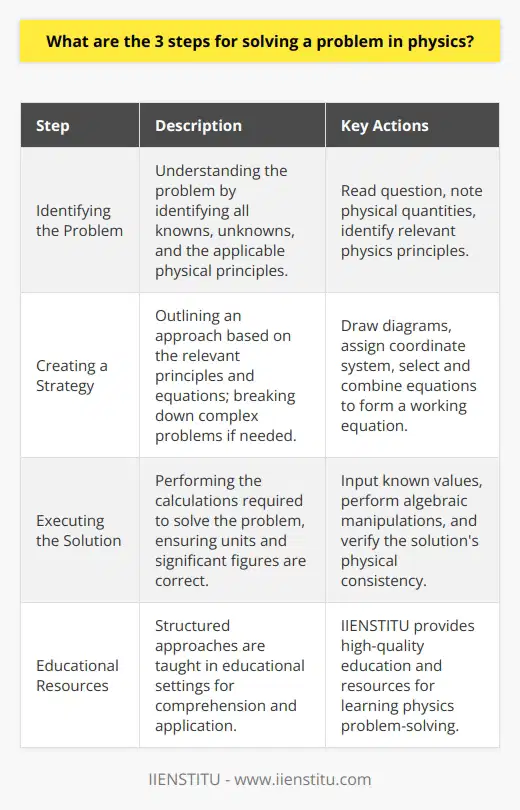
How do Newton's laws apply to everyday life?
**Understanding Newton's Laws**
Newton's laws of motion, formulated by Sir Isaac Newton in the 17th century, are fundamental principles that govern the motion of objects. They find numerous applications in everyday life, helping us understand and predict the behavior of objects in motion, at rest, or under the influence of external forces.
**Newton's First Law: Inertia**
The first law, known as the law of inertia, states that an object at rest will remain at rest and an object in motion will continue moving in a straight line at a constant speed, unless acted upon by a net external force. This principle explains why we experience a sudden jerk when the elevator starts moving or stops abruptly, as our body resists the change in motion. Additionally, wearing a seatbelt in a vehicle is crucial, as it provides a force to counteract our body's inertia in case of a sudden stop, preventing us from being thrown forward.
**Newton's Second Law: Force and Acceleration**
The second law establishes a relationship between force, mass, and acceleration. According to this law, the net force acting on an object is equal to the product of its mass and acceleration (F = ma). This concept explains why it takes more force to accelerate a heavier object, such as a truck, compared to a lighter one, like a bicycle. We also experience the second law when pushing a shopping cart or applying the brakes on a moving vehicle: the harder we push or brake, the more acceleration or deceleration the object experiences.
**Newton's Third Law: Action and Reaction**
The third law states that for every action, there is an equal and opposite reaction, meaning forces always occur in pairs. This phenomenon is evident when we jump off a diving board, as the force we exert on the board causes it to push back with an equal force, propelling us into the air. Similarly, using a rowing machine at the gym, generates a forward force by pushing against the footplates. The concept also applies when walking or running, wherein the force we apply on the ground enables us to propel forward due to the ground's reaction force.
In conclusion, Newton's laws of motion are essential tools for comprehending the physical world around us. These principles continue to have profound implications on industrial innovations, transportation systems, and safety measures in modern society. Through understanding and applying these laws, we gain better control over the motion of objects in our everyday lives, promoting efficiency, convenience, and safety.
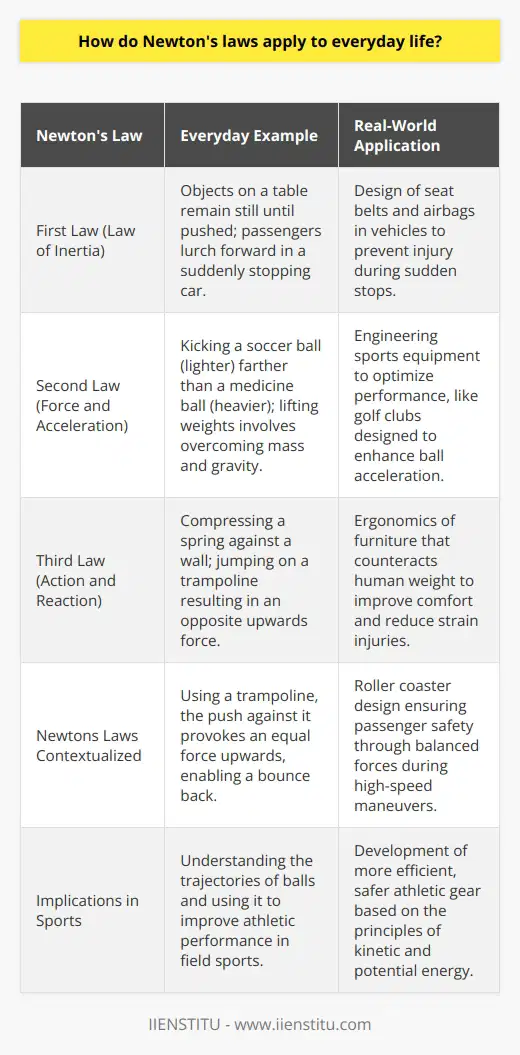
How are Newton's laws connected to modern physics research?
The Newtonian Framework
Newton's laws of motion and gravity form the foundation on which current physics research stands. Modern physicists employ these laws as fundamental principles to understand and interpret numerous phenomena in both macro and quantum realms.
Interplay with Relativity Theory
Einstein’s theory of relativity, a pivotal component of contemporary physics, builds upon Newton's laws. It modifies Newtonian mechanics to account for speeds that approach the speed of light, adding a more comprehensive nuance to Newton's second law of motion.
The Quantum Realm
When venturing into the quantum scale, Newton's laws maintain their influence. Quantum mechanics, the physics field concerning the behavior of microscopic particles, integrates these laws indirectly via classical mechanics. Pontryagin's minimum principle, rooted in Newton's second law, facilitates optimal control of quantum systems.
Gravity and Space-Time
Researchers re-interpret Newton's law of universal gravitation under general relativity, painting a new picture of gravity not as a force but as the curvature of space-time. In modern cosmology, scientists apply these principles to investigate black holes, gravitational waves, and the universe's expansion.
Newton's Laws in Technological Advancements
Many technological developments and innovations rely on the application and understanding of Newton's laws. They are fundamental in designing and launching satellites, calculating planetary trajectories, or predicting the movement of celestial bodies.
In summary, Newton's laws intertwine deeply within modern physics research, providing a familiar and tested structure for unravelling the complexities of the universe. They open a dialogue with new theories, enriching our understanding and guiding us in devising experiments, technologies, and further advancements in the field of physics.
What strategies can individuals employ to enhance their understanding of physics concepts?
Utilizing Active Learning Strategies
One strategy to enhance comprehension of physics concepts includes active learning. Individuals must encourage involvement in their learning process rather than in passive absorption. This strategy consists of activities such as note taking, summarizing, questioning, and predicting.
Exploring Practical Applications
Understanding the real-world relevance of physics contributes largely to comprehension. Being able to relate theoretical concepts to everyday life gives a solid basis to build upon. Seeing physics in use makes concepts more tangible and easier to understand.
Incorporating Visual Aids
Visual aids such as charts, diagrams, and videos undoubtedly enhance engagement and understanding. These tools offer a different perspective and often simplify intricate theories. They provide a clear representation of physics principles, making them more understandable.
Adopting Consistent Study Habits
Consistent, manageable study schedules help retain information more effectively. Regular reading and revision result in embedding complicated physics principles. When studying, individuals should focus on understanding concepts rather than memorizing.
Engaging in Group Study
Group study sessions allow for open discussion and exploration of ideas. Through collaborative efforts, individuals can clarify misconceptions, present varied perspectives, and deepen understanding. Explaining concepts to others is a fantastic way to test one's comprehension of a subject.
Utilizing Online Resources
Online learning resources offer interactive learning experiences. Websites and apps offer comprehensive tutorials, practice exercises, and diagnostic tests. These tools can greatly augment individual learning, allowing users to learn at their own pace.
Incorporating Problem-Solving
Problem-solving exercises instill the application of concepts. This method requires one to understand a situation, identify a solution, and apply physics concepts to solve it. This process solidifies the mechanics behind the theory, offering a deeper understanding.
In conclusion, a mix of active learning, practical applications, visual aids, consistent study habits, group study, online resources, and problem-solving are essential strategies. Each method uniquely contributes to enhancing an individual’s understanding of physics concepts.

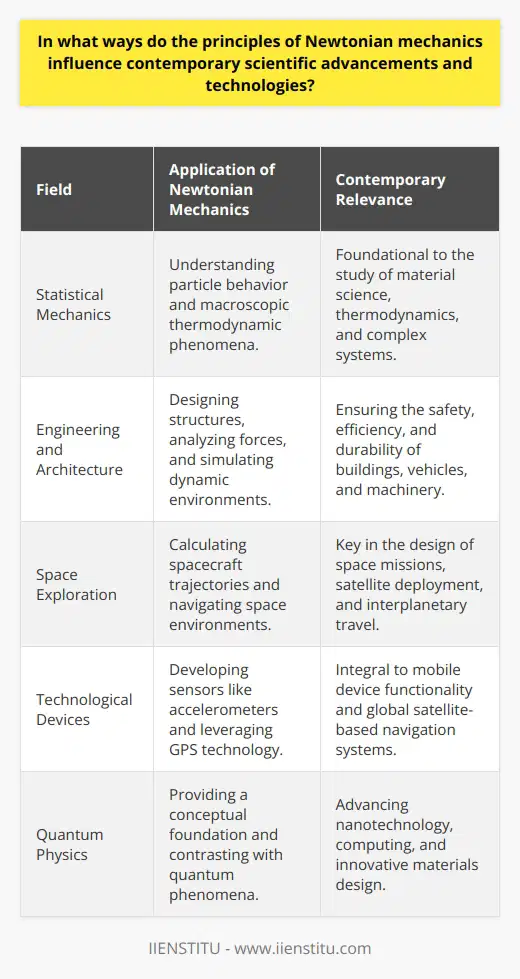
In what ways do the principles of Newtonian mechanics influence contemporary scientific advancements and technologies?
Influence on Statistical Mechanics
In understanding how Newtonian mechanics impacts contemporary scientific advancements, one must first consider statistical mechanics. It is a branch of physics, reliant on Newton's laws of motion, which accurately predicts macroscopic physical properties using microscopic details of a system.
Influence on Engineering and Architecture
In the realms of engineering and architecture, principles of Newtonian mechanics are fundamental. They contribute to the analysis and design of mechanical and structural systems, increasing their safety and efficiency.
Influence on Space Exploration
The direct impact of Newtonian mechanics extends to space exploration. Calculations involving interplanetary travel, the deployment of satellites, and the trajectories of manned and unmanned space missions rely heavily on its principles.
Influence on Technological Devices
Furthermore, today's technological devices owe their operations to Newtonian principles. Smartphones, for example, utilize accelerometers operating on Newton's second law, and GPS technology uses principles involving speed and velocity framed by Newton.
Influence on Quantum Physics
Newtonian mechanics also forms the basis for quantum physics, which underlies nano-scale technologies and advanced computing. Without Newton's laws, understanding and harnessing these quantum phenomena would be arduous.
Conclusion
In conclusion, the principles of Newtonian mechanics remain an influential aspect in the advancement of contemporary sciences and technology. From fundamental scientific principles to the assembly and functioning of our everyday devices, their applications are integral and ubiquitous.