
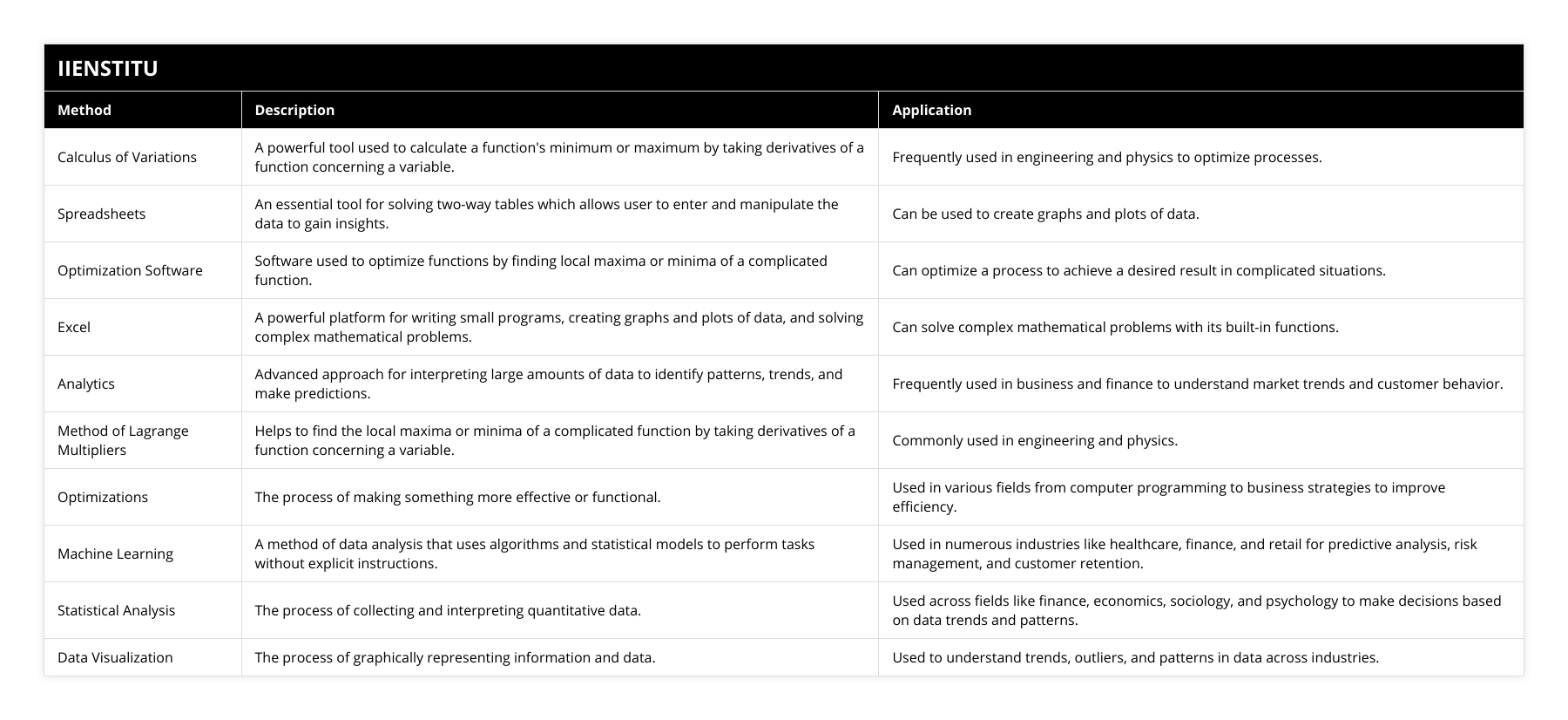
This article discusses various mathematics-based methods for solving complex problems, such as calculus of variations, spreadsheets, optimization software, Excel, analytics, and the process of Lagrange multipliers. Each method has its strengths and weaknesses, and it is essential to choose the right one for the problem.
Introduction
Calculus of Variations
Spreadsheets
Optimization Software
Conclusion
Introduction: When it comes to using quantitative methods to solve complex problems, many well-defined and easy-to-access mathematics-based options are available. This article will discuss the calculus of variations, spreadsheets, optimization software, and Excel as potential solutions. We will also explore the use of analytics to make sense of data and the method of Lagrange multipliers for local maxima and minima of complicated functions.
Calculus of Variations
Calculus of variations is a form of calculus used to determine a function's minimum or maximum. It is a powerful tool for solving problems related to the optimization of processes. It involves taking derivatives of a function concerning a variable and then finding the minimum or maximum of the resulting equation. This method is often used in engineering and physics to solve problems.
Spreadsheets
Spreadsheets are an essential tool for solving two-way tables. They allow the user to enter data into a table and manipulate it to gain insights. Spreadsheets can also be used to create graphs and plots of data.
Optimization Software
The optimization software is used to optimize functions. It is a powerful tool for finding a complicated function's local maxima or minima. It can also optimize a process to achieve the desired result.
Comprehensive Systems Thinking Approach To Complex Problems Solutions
Comprehensive Guide For Fishbone Diagrams İn Decision Making
Excel
Excel is a powerful tool for writing small programs. It can be used to create graphs and plots of data and write small programs. Excel also has several built-in functions that can be used to solve complex mathematical problems.
Analytics
Analytics is a powerful tool for making sense of large amounts of data. It can be used to find patterns in data, identify trends, and make predictions. For example, it is often used in business and finance to gain insights into customer behavior and market trends.
Method of Lagrange Multipliers
The method of Lagrange multipliers is a powerful tool for finding the local maxima or minima of a complicated function. It involves taking derivatives of a function concerning a variable and then finding the minimum or maximum of the resulting equation. This method is often used in engineering and physics to solve problems.
Conclusion: In conclusion, several well-defined mathematics-based methods can be used to solve complex problems. These include the calculus of variations, spreadsheets, optimization software, Excel, analytics, and the process of Lagrange multipliers. Each method has its strengths and weaknesses, and it is essential to choose the right one for the problem.
Unlock your problem-solving skills and unlock the door to success in math and statistics.
Frequently Asked Questions
What topics are covered in the Unlock Your Problem Solving Skills: Definitive Math & Statistics blog post?
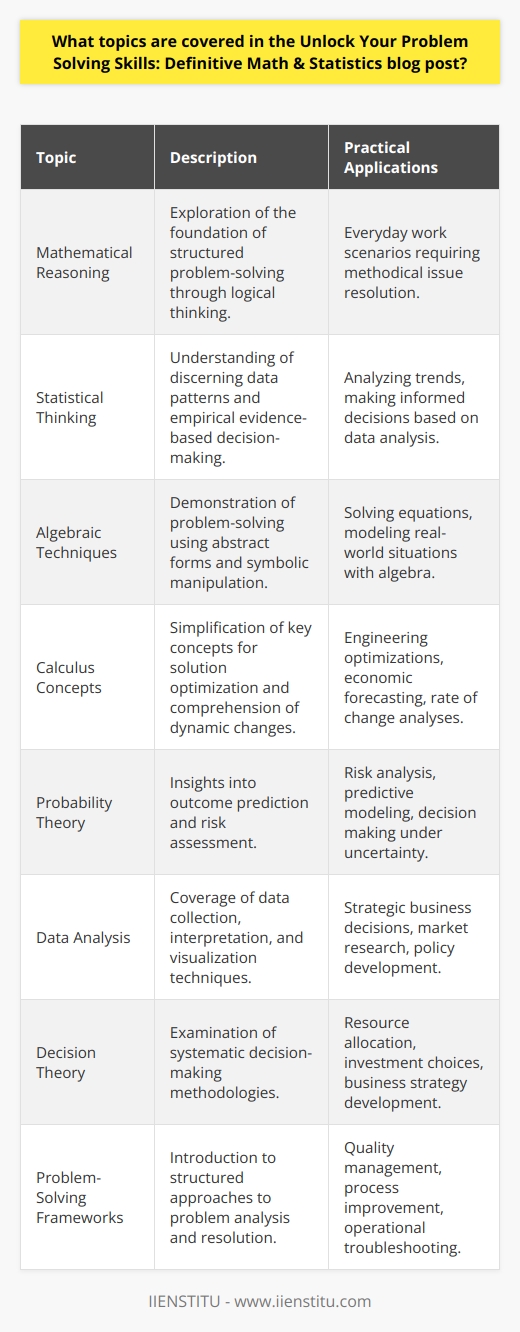
This blog post provides a comprehensive overview of mathematics and statistics related to problem-solving skills. The blog post begins by highlighting the importance of problem-solving skills and the need for them in the modern workplace. It then delves into the various topics covered in the blog post, including:
Methods for solving problems: This section covers various methods for solving problems, such as using logic, analyzing data, and using algorithms. It also provides examples of how these methods can solve real-world problems.
Mathematical fundamentals: This section covers the fundamentals of mathematics, including topics such as algebra, calculus, and geometry. It also provides examples of how these fundamentals can be used to solve problems.
Statistical thinking: This section covers various topics related to statistical thinking, such as descriptive statistics, inferential statistics, and probability. It also provides examples of how these concepts can be used to solve problems.
Problem-solving strategies: This section covers various methods for problem-solving, such as brainstorming, analyzing data, and using algorithms. It also provides examples of how these strategies can solve problems.
Finally, the blog post provides a summary of the main topics covered and offers a few tips for improving problem-solving skills. This blog post provides a comprehensive overview of mathematics and statistics-related problem-solving skills. In addition, it offers a clear and concise explanation of the topics covered and examples of how these topics can be used to solve real-world problems.
How can calculus of variations and spreadsheets be used to improve problem solving skills?
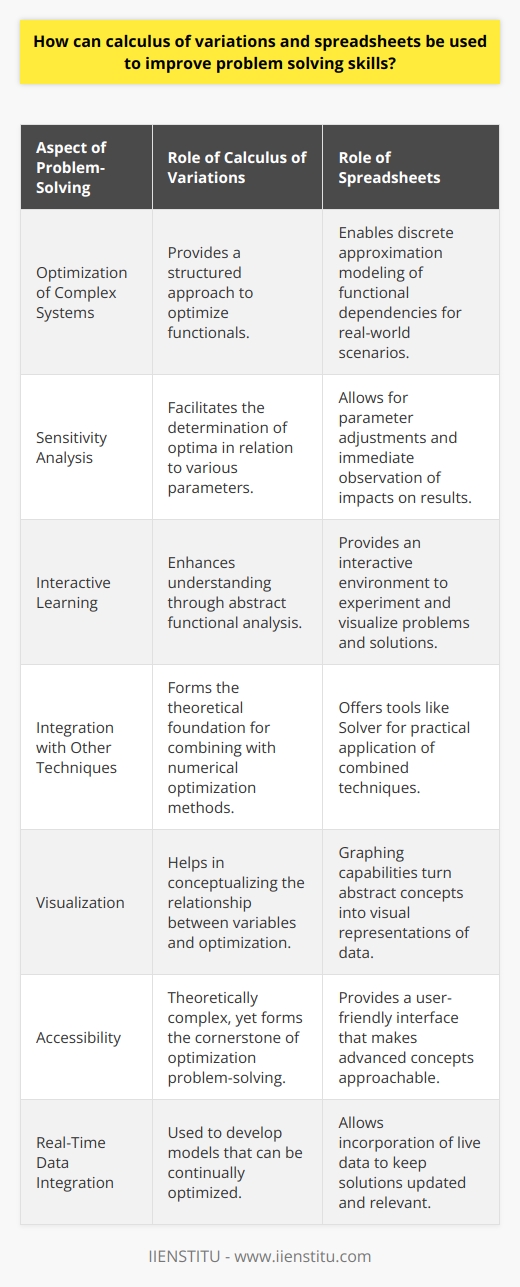
Using the calculus of variations and spreadsheets can be a powerful tool to improve problem-solving skills. Calculus of variations studies the properties of functions that minimize or maximize a given function or are part of several independent variables. It is a powerful tool for solving problems in mathematics, physics, engineering, economics, and other fields. Spreadsheets are also a powerful tool for problem-solving, as they can be used to store and analyze large amounts of data quickly and accurately.
When used together, calculus of variations and spreadsheets can be powerful tools for problem-solving. Calculus of variations can provide a framework for understanding how to optimize a given problem and can help identify the best solution. Spreadsheets can store and analyze large amounts of data quickly and accurately, allowing for a quick and efficient evaluation of the different solutions.
Calculus of variations can solve many problems, including optimization problems, differential equations, and even optimization problems with multiple objectives. Using the calculus of variations, it is possible to find the best solution to a given situation and identify the best solution in terms of cost, time, and other factors. Furthermore, spreadsheets can store and analyze large amounts of data quickly and accurately, allowing for a quick and efficient evaluation of the different solutions.
Using the calculus of variations and spreadsheets together can help improve problem-solving skills by providing a framework for optimizing a given situation and a way to quickly and efficiently evaluate the different solutions. Additionally, spreadsheets can store and analyze large amounts of data quickly and accurately, allowing for a quick and efficient evaluation of the other solutions.
In summary, the calculus of variations and spreadsheets can be a powerful tool for problem-solving, as they provide a framework for understanding how to optimize a given situation and a way to quickly and efficiently evaluate the different solutions. Using these two tools together makes it possible to improve problem-solving skills and find the best solution to a given situation.
What optimization software is recommended for problem solving?
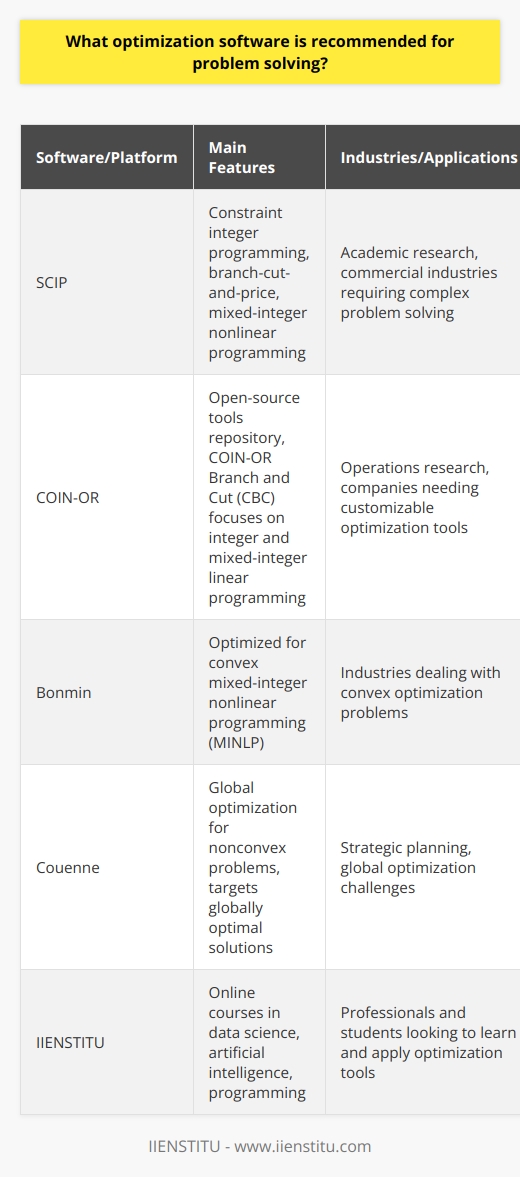
Problem-solving is an essential part of modern business and requires the use of reliable software to help ensure that the process is carried out effectively. Optimization software, in particular, is a powerful tool for solving problems as it enables users to optimize their operations, reduce costs, and make their businesses more efficient. In this blog post, we will discuss some of the best optimization software available for problem-solving.
One of the most popular optimization software packages is CPLEX Optimizer. This software enables users to solve many optimization problems, such as linear, mixed-integer, quadratic, and nonlinear programming. It also provides a user-friendly interface and advanced features, such as constraint-based and global optimization. In addition, CPLEX Optimizer is compatible with various programming languages, making it easy to integrate into existing software.
Another popular optimization software package is Gurobi Optimizer. This software package offers a range of features, such as solving linear programming, quadratic programming, mixed-integer programming, and nonlinear programming problems. It also provides advanced features, such as multi-objective optimization and constraint-based optimization. Furthermore, Gurobi Optimizer is compatible with various programming languages, making it an ideal choice for problem-solving.
Finally, MATLAB Optimization Toolbox is another popular optimization software package. This software enables users to solve many optimization problems, such as linear programming, nonlinear programming, and mixed-integer programming. It also provides an easy-to-use graphical user interface and advanced features, such as global and constraint-based optimization. In addition, MATLAB Optimization Toolbox is compatible with a variety of programming languages, making it easy to integrate into existing software.
In conclusion, various optimization software packages are available for problem-solving, including CPLEX Optimizer, Gurobi Optimizer, and MATLAB Optimization Toolbox. Each software package offers a range of features and is compatible with various programming languages, making them ideal for problem-solving.
How do you develop math problem-solving skills?
Understanding Math Concepts
To develop math problem-solving skills, it is essential to first understand the underlying mathematical concepts. This involves studying and grasping essential principles, such as basic operations, factors, and multiples, as well as advanced theories like geometry, calculus, and algebra. A strong foundation in these concepts paves the way for effective problem-solving.
Engaging in Regular Practice
Regular practice is vital for honing math problem-solving skills. Setting aside dedicated time to complete math exercises on a daily basis enables gradual improvement and fosters long-term retention of mathematical concepts. The consistent practice also helps in identifying areas that require further improvement or clarification, providing opportunities for targeted learning.
Applying Different Strategies
Employing a variety of problem-solving strategies enhances one's ability to tackle diverse math problems. Strategies such as drawing diagrams, using trial and error, identifying patterns and employing logical reasoning aid in navigating complex problems. Experimenting with different approaches enables the discovery of preferred and efficient problem-solving methods.
Working through Examples
Working through solved examples is an effective way to develop math problem-solving skills. Doing so not only demonstrates the application of the concepts but also exposes different strategies for solving problems. Examining worked examples closely helps in identifying key steps and mistakes to avoid, thus enhancing one's problem-solving capability.
Collaborating with Peers
Collaborating with peers and engaging in group study sessions provide opportunities to learn from others, exchange problem-solving strategies, and receive valuable feedback. Discussing difficult problems with peers fosters critical thinking and helps in viewing problems from diverse perspectives, leading to better problem-solving skills.
Seeking Help from Teachers and Mentors
When encountering difficulties in solving math problems, seeking guidance from teachers or mentors is crucial. These experienced individuals can offer invaluable assistance and help in identifying misconceptions or gaps in knowledge. Their explanations and clarifications contribute significantly to the development of robust math problem-solving skills.
In conclusion, developing math problem-solving skills requires a clear understanding of mathematical concepts, regular practice, the employment of diverse strategies, analysis of solved examples, collaboration with peers, and guidance from experienced mentors. By incorporating these elements into one's study routine, one can continually enhance their math problem-solving abilities and excel in the subject.

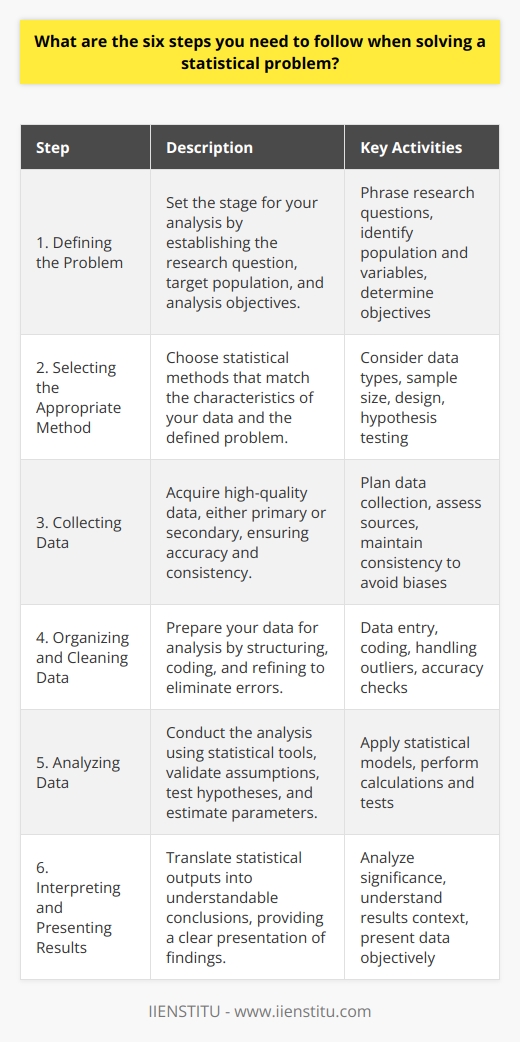
What are the six steps you need to follow when solving a statistical problem?
Defining the Problem
The first step in solving a statistical problem is to define the problem clearly. This involves identifying the research question, specifying the population of interest, and determining the purpose of the analysis.
Selecting the Appropriate Method
Once the problem is defined, the next step is to choose an appropriate statistical method to analyze the data. This choice depends on the type of data, research question, and the purpose of the analysis. It is important to ensure that the selected method is suitable for the problem to obtain valid and reliable results.
Collecting Data
Data collection is a critical step in the process, as the quality of the collected data directly impacts the accuracy and validity of the analysis. There are various methods to collect data, such as surveys, experiments, observational studies, and secondary sources. The chosen method should align with the research question and the population of interest to ensure that the data is representative and relevant to the problem.
Organizing and Cleaning Data
After collecting the data, the next step is to organize and clean the data for analysis. This involves checking for errors and inconsistencies, assessing missing values, and ensuring that the data is in a format suitable for the chosen statistical method. Proper organization and cleaning of the data help to prevent errors in analysis and improve the reliability of the results.
Analyzing Data
Once the data is organized and cleaned, the next step is to analyze it using the chosen statistical method. This involves performing calculations, conducting hypothesis tests, and estimating parameters or relationships based on the data. The process of data analysis aims to answer the research question and provide insights into the problem under investigation.
Interpreting and Presenting Results
The final step in solving a statistical problem is interpreting and presenting the results of the analysis. This requires evaluating the significance of the results, drawing conclusions, and explaining the findings in the context of the problem. Presenting the results in a clear and concise manner allows others to understand the implications of the research and how it contributes to the broader field of study.
What are the problem solving skills in mathematics?
Defining Problem Solving Skills in Mathematics
Problem solving skills in mathematics are essential cognitive abilities that enable learners to effectively approach, analyze, and resolve various mathematical challenges. These skills encompass a systematic process that encompasses numerous strategies and techniques.
Strategies for Mathematical Problem Solving
Understanding the problem: A student must first comprehend the problem by breaking it down into smaller parts or sub-problems, and then, identify the important information needed to tackle it.
Devising a plan: Once the student understands the problem, they create a plan of action by selecting the appropriate strategies and mathematical tools, such as formulas or algorithms, to address it.
Executing the plan: The student applies the selected strategies and tools, solving the problem step-by-step while maintaining accuracy and precision in their calculations.
Evaluating the solution: The student checks the validity of their solution, comparing it with the original problem to ensure that it is logical and accurate.
Reflecting on the process: To improve their problem solving skills further, students review the entire process, identifying successful strategies and potential areas for improvement.
Enhancing Problem Solving Skills through Instruction
Mathematical problem solving skills can be honed through explicit instruction, modeling, and practice in the context of real-world scenarios. Teachers should encourage students to think critically, share their reasoning, and collaborate with peers to reach a deeper understanding of the problem-solving process. By fostering a positive and supportive learning environment, educators can build students' confidence in their abilities and promote the development of these crucial skills.

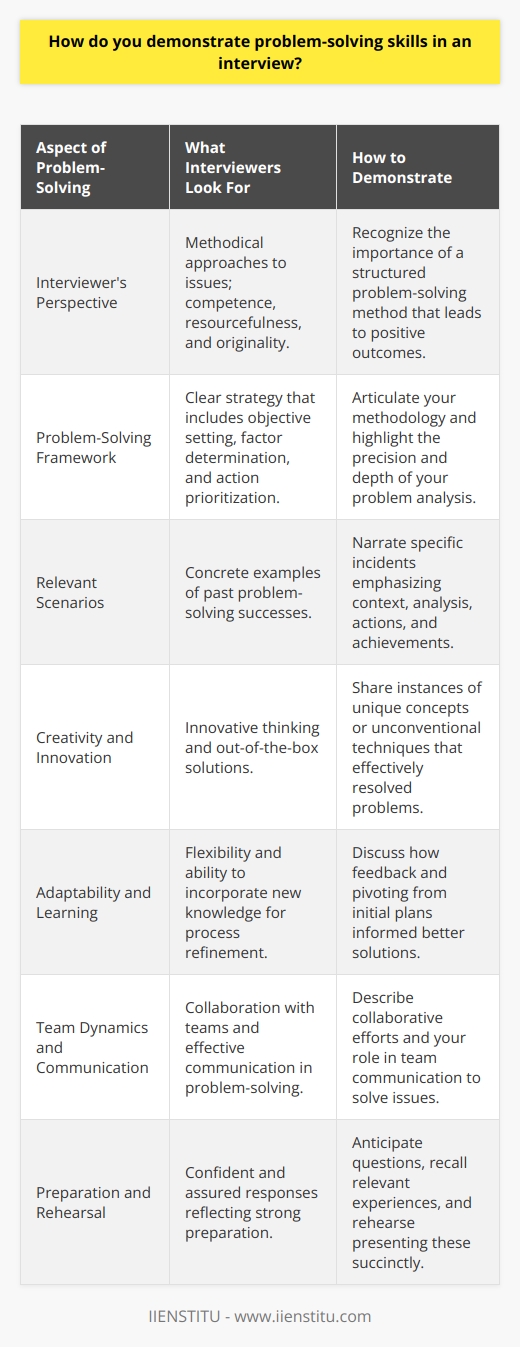
How do you demonstrate problem-solving skills in an interview?
Demonstrating Problem-Solving Skills in an Interview
Understanding Interview Expectations
In an interview setting, it is essential to grasp the expectations of potential employers. Demonstrating problem-solving skills involves showcasing the ability to approach difficult situations, logically assess available information, and deliver effective resolutions. Interviewers often present hypothetical or real-life scenarios to evaluate how well an applicant can handle challenges.
Breaking Down Problems
How a candidate dissects a problem is crucial in forming a viable solution. Structured thinking, breaking down problems into smaller, more manageable parts, and identifying the root cause can showcase organized and effective thought processes. Employing this approach demonstrates analytical and critical thinking abilities, which are highly valued by many industries.
Applying Relevant Experience
Leveraging personal experiences relevant to the specific problem can prove useful in highlighting past successes in overcoming challenges. When discussing past experiences, it is important to focus on the actions taken, challenges faced, and results achieved. Specific examples from previous work or academic experiences can provide tangible evidence of the candidate's problem-solving capabilities.
Employing Creative Approaches
Creativity is a vital element in problem-solving. Demonstrating original and innovative ideas in response to potential obstacles can set a candidate apart from the competition. Engaging the interviewer with inventive thought processes can be as simple as reframing their question or proposing alternative solutions they may not have considered.
Adaptability and Flexibility
When tackling complex issues, sometimes the initial solution is not the most effective. It is essential to demonstrate adaptability and willingness to change strategies when necessary. Communicating flexibility and openness to different approaches can convince interviewers of a candidate's ability to problem-solve in varying situations.
Collaboration and Communication
Problem-solving often requires collaboration with others. An essential component of this skill is the ability to communicate ideas and facilitate teamwork. Collaborative examples from past experiences or suggestions of how to work with others to resolve potential issues convey a candidate's ability to thrive within a team environment.
Preparing for Problem-Solving Questions
To excel in an interview, one should prepare beforehand for potential problem-solving questions. Identifying critical experiences, practicing articulating them succinctly, and exhibiting a willingness to learn from past challenges can demonstrate a candidate's readiness to tackle future obstacles.
In conclusion, effectively showcasing problem-solving skills in an interview involves understanding the expectations, employing structured and adaptable thought processes, communicating relevant experiences, and exhibiting creativity when addressing potential challenges. Preparation and confidence in one's abilities can be instrumental in securing a position that requires strong problem-solving skills.
What are some examples of problem-solving skills?
Analytical Thinking
One example of problem-solving skills is analytical thinking, which involves breaking down complex issues into manageable components. This allows individuals to identify the root cause of a problem and devise potential solutions.
Critical Thinking
Critical thinking, another problem-solving skill, involves objectively evaluating information to determine whether it is credible and relevant. This process allows individuals to make informed decisions and consider multiple perspectives before selecting a solution.
Creative Thinking
Creative thinking is essential for developing innovative solutions to problems. This skill encourages individuals to think outside the box and consider unorthodox approaches that may not have been previously considered.
Decision Making
Effective problem-solving also depends on sound decision-making abilities. This skill requires weighing the pros and cons of various solutions and selecting the best course of action based on the available information.
Research Skills
Strong research skills play a crucial role in the problem-solving process. Individuals must be able to gather relevant information from various sources, evaluate its credibility, and utilize it to better understand a given problem and develop potential solutions.
Collaboration and Communication
Working with others is often necessary for solving complex problems. This requires strong collaboration and communication skills, enabling individuals to effectively contribute their ideas, listen to various perspectives, and adapt their approach based on the group's input.
Adaptability and Flexibility
Problem-solving also demands adaptability and flexibility, as circumstances often change, requiring individuals to alter their strategies. These skills involve modifying one's approach when new information emerges or when unforeseen obstacles arise.
Emotional Intelligence
Emotional intelligence, or the ability to recognize and manage one's emotions and those of others, can significantly impact problem-solving success. This skill enables individuals to approach problems with a clear, focused mindset and navigate challenging situations with resilience.
Learning from Failure
Lastly, effective problem solvers must possess the ability to learn from failure. They should be able to acknowledge when an approach did not work, analyze the reasons behind it, and modify their strategy accordingly moving forward.

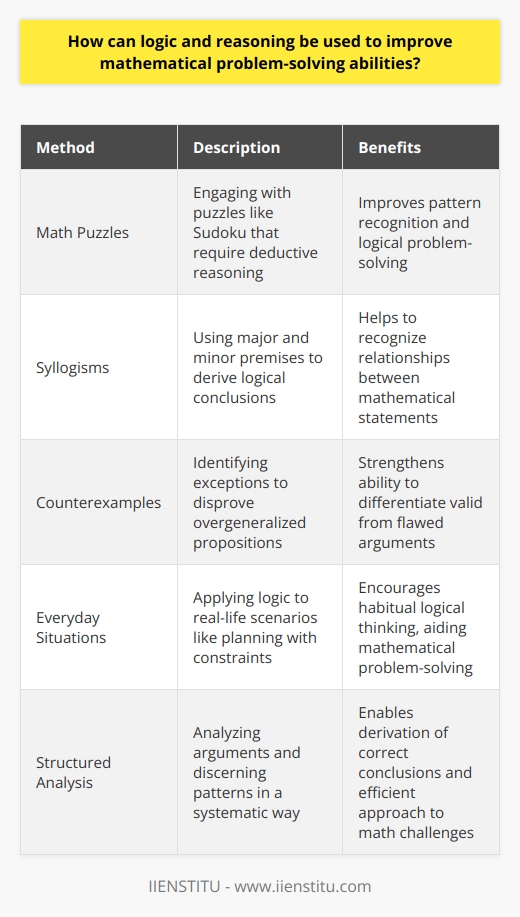
How can logic and reasoning be used to improve mathematical problem-solving abilities?
Developing Logical Thinking Skills
Logic and reasoning play a critical role in enhancing mathematical problem-solving abilities. The foundation of logic consists of understanding how to structure arguments, identify patterns, and form correct conclusions based on premises.
Practicing Math Puzzles
By engaging with mathematical puzzles, one improves their ability to apply logical thinking. These puzzles range from Sudoku to logic grid puzzles, which generally require the solver to use deductive reasoning to identify a solution. This practice hones our skills in pattern recognition and logical deduction, which then translate to improved problem-solving abilities in other mathematical domains.
Using Syllogisms in Mathematics
Syllogisms are logic exercises that help in understanding the relationships between statements. They involve a major premise, a minor premise, and a conclusion. For example, if 'all circles are round' (major premise) and 'shape A is a circle' (minor premise), you can deduce that 'shape A is round' (conclusion). This concept can be extended to abstract mathematics by analyzing patterns and relationships between numbers and variables.
Evaluating Counterexamples
Assessing counterexamples is another useful method for solidifying logical concepts in mathematics. A counterexample is an instance where a statement's premise is true, but the conclusion is false. For example, the statement 'all prime numbers are odd' is disproven by the counterexample of the number 2, which is both prime and even. By working through counterexamples, we strengthen our logical reasoning and become more adept at identifying incorrect premises or conclusions.
Applying Logic to Real-life Scenarios
Applying logical reasoning beyond the classroom is essential in developing mathematical problem-solving abilities. For example, consider planning a travel itinerary with specific constraints, such as budget or time. This scenario would require one to efficiently allocate resources and make decisions based on logical reasoning. Incorporating these skills into daily life can improve mathematical problem-solving abilities by reinforcing logical thinking habits.
In conclusion, enhancing logical thinking skills through puzzles, syllogisms, counterexamples, and applying them to real-life scenarios can lead to improvements in mathematical problem-solving abilities. By embracing these strategies, individuals cultivate essential reasoning skills that contribute significantly to achieving success in mathematics and beyond.
What are the key components of effective mathematical problem-solving strategies?
Understanding the Problem
The first component of efficient problem-solving in mathematics is understanding the problem. This phase involves interpreting the problem and identifying what the problem asks.
Devising a Plan
Once learners understand a problem, they should devise a plan of action. The plan can derive from recalling similar problems, rephrasing the problem, breaking the task into smaller manageable parts, or creating diagrams.
Implementing the Plan
The next stage is the execution of the plan. It involves applying mathematical knowledge and techniques to problem-solving. Informative note-taking, systematic computations, and use of suitable algorithms occur in this stage.
Checking the Answer
Lastly, checking the answer is a vital step that confirms the rightness of the final result. Reviewing the calculations and reasoning or checking the answer against the problem statement helps achieve accurate results.
Reflection on the Problem-solving Process
Reflection forms an integral part of mathematical problem-solving. Through reflection, students evaluate the effectiveness of their strategies, which promotes learning from mistakes and successes.
In conclusion, effective mathematical problem-solving strategies consist of understanding the problem, devising a plan, implementing the plan, checking the answer, and reflection. These key components ensure a systemic, structured and analytical approach to tackling mathematical problems.

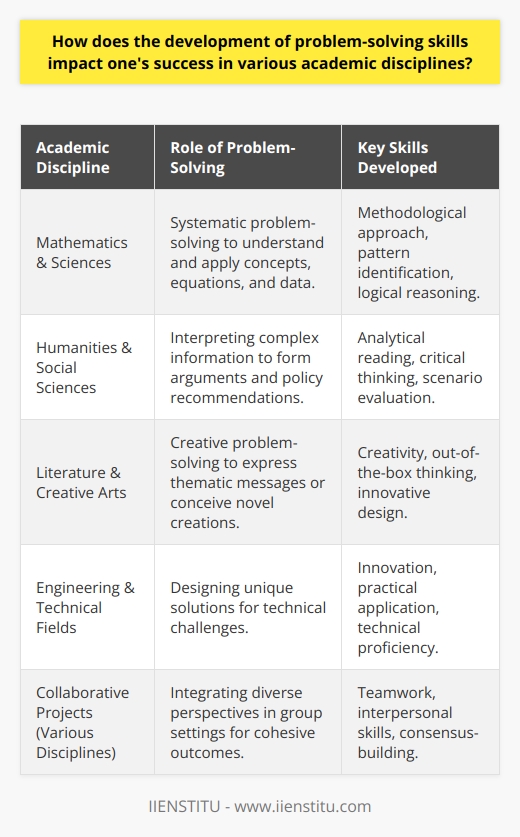
How does the development of problem-solving skills impact one's success in various academic disciplines?
Role of Problem-Solving Skills in Academic Success
Problem-solving skills play a pivotal role in one's academic success. They are invaluable tools in virtually every field of study. Regardless of the discipline, scholars frequently encounter complex situations that require analytical thinking.
Impact on Math and Science Disciplines
In disciplines such as Math and Science, profound problem-solving skills enable students to deconstruct complex tasks, further promoting understanding. This is crucial in these fields because understanding the problem is the first step towards finding the solution.
Impact on Humanities and Social Sciences
In Humanities and Social Sciences, problem-solving skills help students analyze different viewpoints to make reasoned arguments. These disciplines often demand a subtle form of problem-solving skills, including dissecting arguments, assessing evidence, and crafting persuasive positions.
Facilitating Critical Thinking
Critical thinking often serves as a prerequisite for effective problem-solving. It requires the student to evaluate data critically, process information in a logical way, and make decisions based on evidence, essential across all academic disciplines.
Promoting Creativity
Problem-solving also encourages creativity. For instance, problem-solving in subjects such as arts or literature often demands novel thinking. This fuels creativity, which can translate to academic success in such disciplines.
Incorporating Teamwork
In disciplines that involve group work, problem-solving skills can foster better teamwork. The ability to analyze and resolve group conflicts or problems contributes to a productive work environment and leads to higher-quality group performance.
In conclusion, the development of problem-solving skills is an essential ingredient of academic success across various disciplines. Problem-solving fosters critical thinking, encourages creativity, and supports effective teamwork, all of which are significant contributors to academic achievement.
In what ways can the art of problem solving approach be applied to real-world situations outside of mathematics?
Problem-Solving Application in Career Fields
The art of problem-solving indeed extends beyond mathematics and is applicable in various real-world situations. For instance, in the field of business, executives often use problem-solving strategies to tackle complex project management tasks, devise marketing strategies, or improve operational efficiency.
Approach in Negotiation Scenarios
Negotiations also hinge on problem-solving approaches, specifically when creating win-win situations. As parties aim for mutually beneficial outcomes, strategic problem solving allows negotiators to comprehend the needs, preferences and limitations of all involved effectively.
Relevance in Personal Life
The approach also proves invaluable for handling personal challenges and making crucial life decisions. It encourages individuals to evaluate different aspects of a problem, consider various solutions, and make a decision that best suits their personal circumstances.
Usage in Public Policy
Lastly, problem-solving plays a critical role in shaping public policies. Policymakers need to identify societal issues, conceive possible solutions, and employ critical thinking skills to select the most effective strategies.
In essence, the art of problem-solving serves as a versatile tool usable in various life contexts, for career advancements, personal growth, and societal development. Therefore, mastering this skill forms an integral part of lifelong learning and success.



