In our increasingly interconnected world, we often find ourselves entangled in a myriad of relationships and systems that can be overwhelming to comprehend. It's like navigating through a dense forest, where every tree is connected to another in ways that are not always apparent. Traditional analysis methods sometimes fall short when faced with the depth of these complexities. That's where tools like interrelationship digraphs come into play.
I remember the first time I encountered the concept of interrelationship digraphs. It was during a project management course I took years ago. The instructor, a seasoned professional with decades of experience, introduced us to this tool as a way to visualize and analyze complex problems. At first, I was skeptical. I thought, "How can a simple diagram with nodes and arrows help me understand something as intricate as a large-scale project?" But as we delved deeper into the topic, I began to see the power and versatility of this approach.
Interrelationship digraphs, also known as directed graphs or digraphs, are visual representations of the relationships between different elements in a system. They consist of nodes, which represent the elements, and arrows, which indicate the direction of influence or causality between these elements. What sets digraphs apart from regular graphs is their emphasis on the directionality of relationships. In a digraph, an arrow from node A to node B means that A influences B, but not necessarily the other way around. This is crucial in understanding cause-and-effect scenarios and identifying key drivers in a system.
One of the key benefits of using digraphs in problem-solving is their ability to reveal hidden connections and dependencies. In complex systems, it's easy to focus on the obvious relationships and miss the subtle, indirect influences that can have a significant impact. By mapping out all the elements and their connections in a digraph, we can uncover these hidden links and gain a more comprehensive understanding of the problem at hand.
For example, let's say you're a teacher trying to improve student performance in your class. You might start by identifying the factors that directly influence student learning, such as teaching methods, classroom environment, and student motivation. However, a digraph analysis might reveal that student motivation is indirectly affected by factors like parental involvement, peer influence, and extracurricular activities. By visualizing these complex relationships with digraphs, you can develop a more holistic approach to enhancing student learning.
Creating an interrelationship digraph is a straightforward process that can be adapted to any problem or system. The first step is to identify all the relevant elements involved. These could be factors, stakeholders, or components, depending on the context. Next, you determine the relationships between these elements, asking questions like "Does A influence B?" or "Is there a cause-and-effect relationship between C and D?" Once you have established the directionality of each relationship, you can start drawing the digraph, with nodes representing the elements and arrows indicating the direction of influence.
One of my favorite examples of interrelationship digraph application comes from the field of ecology. Ecosystems are incredibly complex, with numerous species interacting in intricate ways. A change in one species' population can have far-reaching effects on the entire ecosystem. By using digraphs, ecologists can map out these interactions and predict the impact of disturbances or interventions. For instance, a digraph of a grassland ecosystem might show how a decrease in the population of a keystone species, like wolves, can lead to an overabundance of their prey, such as deer, which in turn can overgraze the vegetation and alter the landscape. Understanding these digraphs and directed graphs allows ecologists to develop more effective conservation strategies and manage ecosystems sustainably.
Interrelationship digraphs have found applications in various fields, from project management to education, healthcare, and business. In project management, digraphs can help identify critical paths and dependencies, allowing managers to prioritize tasks and allocate resources effectively. In healthcare, digraphs can be used to map out patient journeys, identifying bottlenecks and opportunities for improvement in the care delivery process. Educators can use digraphs to design curriculum maps, ensuring that learning objectives are properly sequenced and integrated.
One of the most powerful aspects of interrelationship digraphs is their ability to visualize feedback loops. Feedback loops occur when the output of a system influences its input, creating a self-reinforcing or self-correcting cycle. Positive feedback loops amplify change, while negative feedback loops counteract it. In a digraph, feedback loops appear as circular paths, where an element indirectly influences itself through a chain of other elements. Identifying these loops is crucial for understanding the dynamics of a system and predicting its behavior over time.
For instance, consider the feedback loops in climate change. As the Earth's temperature rises due to greenhouse gas emissions, it causes ice caps to melt, reducing the planet's albedo (reflectivity). This, in turn, leads to more solar energy being absorbed, further increasing the temperature. This positive feedback loop accelerates the warming process, making it harder to mitigate climate change. By visualizing these loops in an interrelationship digraph, policymakers and scientists can develop more effective strategies to break the cycle and address the root causes of the problem.
Interrelationship digraphs are not limited to academic or professional settings. They can be valuable tools for personal decision-making and problem-solving as well. Whenever you face a complex decision or challenge, mapping out the factors and their relationships can provide clarity and insight. It can help you identify the key drivers of the problem, anticipate unintended consequences, and develop more robust solutions.
I once used an interrelationship digraph to navigate a career transition. I was feeling stuck in my job and wanted to explore new opportunities, but I wasn't sure where to start. By creating a digraph of my skills, interests, values, and potential career paths, I was able to see the connections and trade-offs between different options. It became clear that my passion for writing and my experience in marketing could be combined into a role in content strategy. This insight gave me the confidence to pursue a new direction and ultimately led to a fulfilling career change.
In today's data-driven world, interrelationship digraphs are evolving to handle larger and more complex datasets. Software tools and algorithms can now generate digraphs automatically from vast amounts of data, uncovering patterns and relationships that might be invisible to the human eye. These advancements have opened up new possibilities for using digraphs in fields like bioinformatics, social network analysis, and strategic decision-making.
However, it's important to remember that interrelationship digraphs are not a silver bullet. They are a tool for understanding and analyzing complexity, but they do not replace critical thinking and domain expertise. Digraphs can reveal relationships and patterns, but interpreting these insights and translating them into actionable strategies requires human judgment and creativity.
Moreover, creating an effective interrelationship digraph requires careful consideration of the scope and boundaries of the problem. It's easy to get lost in the details and include every possible factor, but this can lead to a cluttered and confusing diagram. The key is to focus on the most relevant and influential elements while maintaining a manageable level of complexity. This often involves iterating and refining the digraph as new insights emerge.
In conclusion, interrelationship digraphs are powerful tools for navigating the complexities of our interconnected world. They provide a visual framework for understanding the relationships and dependencies between elements in a system, revealing hidden connections and feedback loops. By applying digraphs to problem-solving and decision-making, we can gain clarity, anticipate unintended consequences, and develop more effective strategies.
Whether you're an educator looking to design engaging curricula, a healthcare professional seeking to improve patient outcomes, or a business leader making strategic decisions, interrelationship digraphs can be a valuable addition to your toolkit. They encourage systems thinking, foster collaboration, and promote a more holistic approach to problem-solving.
So the next time you face a complex challenge, consider grabbing a pen and paper (or a digital tool) and mapping out an interrelationship digraph. You might be surprised by the insights and solutions that emerge when you visualize the unseen connections that shape our world.
References:
Capra, F. (1996). The Web of Life: A New Scientific Understanding of Living Systems. Anchor Books.
Checkland, P. (1999). Systems Thinking, Systems Practice: Includes a 30-Year Retrospective. John Wiley & Sons.
Meadows, D. H. (2008). Thinking in Systems: A Primer. Chelsea Green Publishing.
Senge, P. M. (2006). The Fifth Discipline: The Art & Practice of The Learning Organization. Currency.
Warfield, J. N. (2006). An Introduction to Systems Science. World Scientific Publishing Company.
Frequently Asked Questions
What constitutes an interrelationship digraph and how does it assist in understanding complex connections?
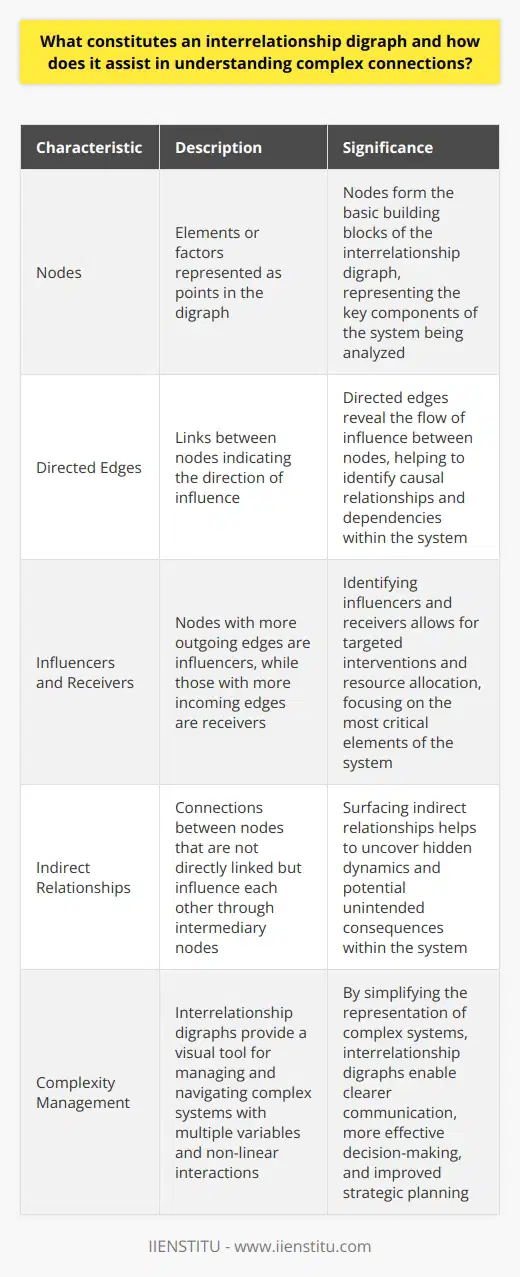
Understanding Interrelationship Digraphs
Interrelationship digraphs form a crucial tool. They help us map and understand complex interactions. In essence, they are visual representations. They capture how various elements influence each other.
Characteristics of Interrelationship Digraphs
These digraphs have specific traits. Each element or factor appears as a node. Nodes link together through directed edges. These edges represent influences. Each node can influence several other nodes. Similarly, it can receive influence from multiple other nodes. The direction of the edge indicates the flow of influence.
Nodes vary in incoming and outgoing edges. More outgoing edges indicate a greater influence. Conversely, more incoming edges suggest greater susceptibility. The digraph thus reveals key influencers and receivers within a system.
Application of Digraphs
Such tools are invaluable for complex analysis. They apply to organizational studies, project management, and more. They allow teams to pinpoint primary factors in a system. Users can thus allocate resources more effectively. The focus typically shifts toward the most influential elements.
Interrelationship digraphs also surface indirect relationships. Users often overlook these in linear analysis. Yet, they play a critical role in system dynamics. The digraphs thus facilitate a deeper understanding of systems.
- Mapping interconnections becomes simpler.
- Identifying causal relationships enhances decision-making.
- Visualizing complex systems aids in communication.
Advantages of Interrelationship Digraphs
Digraphs hold several advantages over other tools. They enable a broader and balanced view. They allow users to recognize multiple interactions. Additionally, they can increase clarity in understanding systems. Such tools are particularly useful when:
- Analyzing systems with many variables.
- Dealing with problems of non-linear nature.
- Exploring scenarios with multiple potential causes.
These digraphs thus assist teams in strategic planning. They inform policy-making and support continuous improvement efforts. They provide a foundation for robust analysis and informed decisions.
Interrelationship digraphs provide clarity. They reveal much about complex systems. Users can manage and navigate intricate connections. This leads to well-informed strategies and beneficial outcomes. Thus, mastering their use is an asset. It makes tackling complex tasks significantly easier.
In building an interrelationship digraph, what are the key steps and elements to consider?
Understanding an Interrelationship Digraph
An interrelationship digraph maps the connections between complex variables. It highlights causes and effects within a system. We use it to visualize dependencies and feedback loops. This tool is valuable in quality management and strategy development.
Key Steps in Building a Digraph
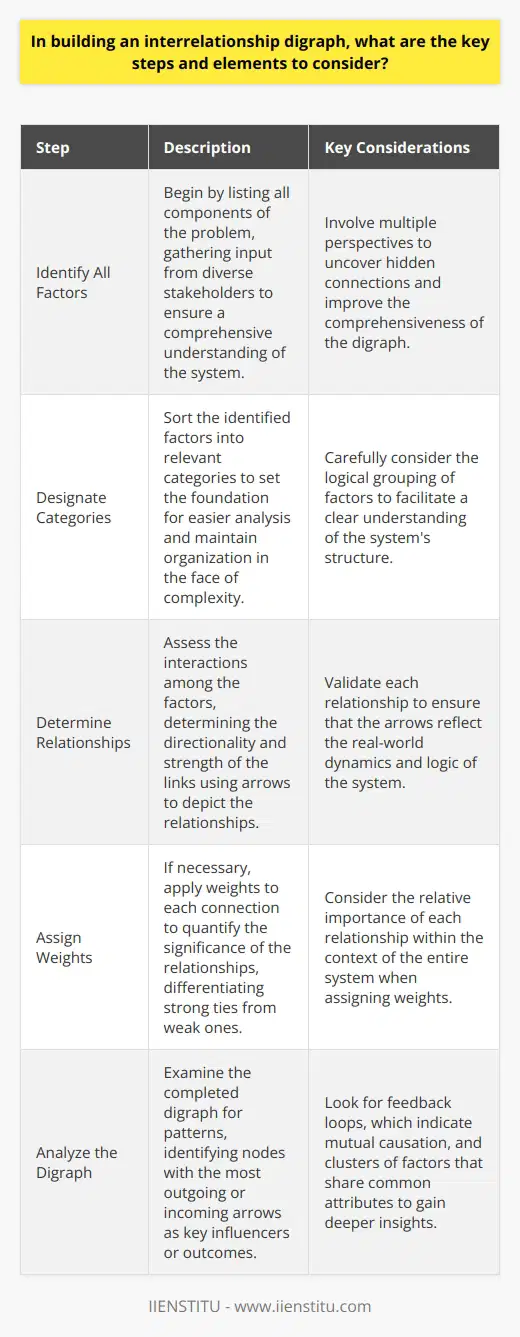
Identify All Factors
Begin with listing components of the problem. Gather input from diverse stakeholders. Consider every possible influencing factor.
Designate Categories
Sort factors into relevant categories. This sets the foundation for easier analysis. It ensures organization prevails in complexity.
Prepare the Digraph
Create a blank matrix or graph. Position the factors as nodes on the diagram. Arrange them discreetly but visibly.
Determine Relationships
Assess interactions among the factors. Determine the directionality and strength of these links. Use arrows to depict the relationships.
Assign Weights
Apply weights to each connection if necessary. This quantifies the significance of each relationship. Differentiate strong ties from weak ones.
Analyze the Digraph
Look for patterns within the connections. Identify nodes with the most outgoing or incoming arrows. These are key influencers or outcomes.
Draw Conclusions
Evaluate the digraph for insights. Make data-driven decisions based on interrelationships. Focus on factors with the greatest impact.
Elements to Consider
Nodes: These represent the factors or variables.
Arrows: They indicate the direction of the relationship.
Weights: Important when quantifying the connection's strength.
Feedback Loops: Cycles indicating mutual causation.
Clustering: Factors that share a common category or attribute.
Constructing the Interrelationship Digraph Effectively
Engage Broad Perspectives
Involving many viewpoints uncovers hidden connections. It improves the comprehensiveness of the digraph.
Simplify When Possible
Use simple symbols and notations. This facilitates easier understanding by a wider audience.
Validate Relationships
Check the logic behind each arrow. Ensure relationships reflect the real-world dynamics.
Keep It Dynamic
Update the digraph over time. This reflects changes in the system or environment.
Utilize Software Tools
Employ digraph software for complex scenarios. They offer dynamic features and optimizations.
An interrelationship digraph requires meticulous construction. It can elucidate complex systems and inform strategic decisions. Employ these steps and elements for effective digraph creation. Consider the power of visual analysis in problem-solving.
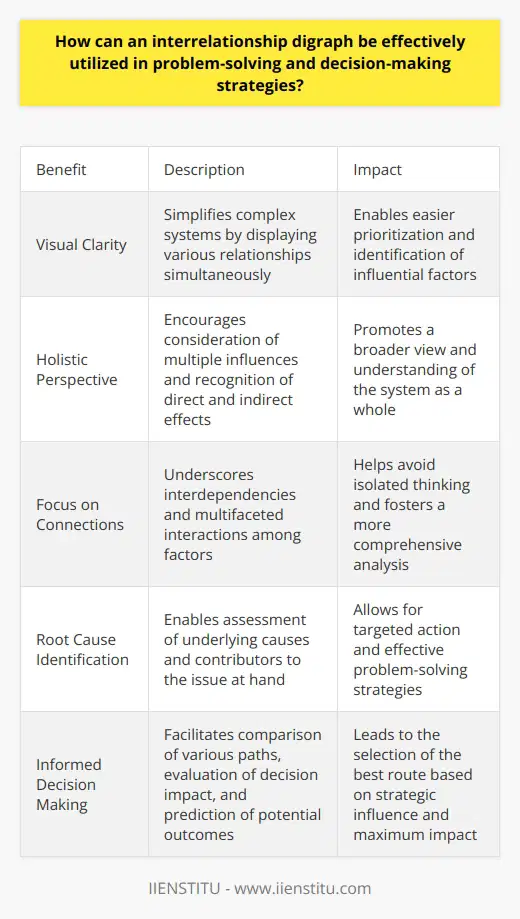
How can an interrelationship digraph be effectively utilized in problem-solving and decision-making strategies?
Understanding Interrelationship Digraphs
An interrelationship digraph maps complex relationships. It visualizes how factors interconnect. Experts use it in diverse fields. It aids in problem-solving and decision-making. This tool highlights causal influences among factors. It clarifies systems thinking.
Benefits of Using an Interrelationship Digraph
Visual Clarity
It simplifies complex systems. Users see various relationships at once. Prioritization becomes easier. Influential factors stand out.
Holistic Perspective
It encourages a broader view. Users consider multiple influences. They recognize direct and indirect effects.
Focus on Connections
The tool underscores interdependencies. Users track multifaceted interactions. They avoid isolated thinking.
Applying the Interrelationship Digraph in Problem-Solving
Identify Components
Users list all relevant factors. They consider every possible influence. Determining connections comes next.
Establish Interrelations
Users draw connections between factors. They denote the nature of relationships. They use arrows to indicate direction.
Analyze Patterns
Users look for significant patterns. They identify the most influential factors. They detect feedback loops.
Determine Root Causes
Users assess underlying causes. They reveal contributors to the issue. Action focuses on these points.
Develop Strategies
Users craft informed strategies. They tackle key factors first. They create action plans.
Utilizing the Interrelationship Digraph in Decision Making
Clarify Goals
Users define clear objectives. They ensure alignment with goals. Decision criteria become apparent.
Weigh Options
Users consider various paths. They compare the impact of decisions. They evaluate based on connections.
Predict Outcomes
Users foresee potential results. They use the digraph's insights. They minimize unintended consequences.
Select Best Route
Users choose informed options. They pick based on strategic influence. They prioritize for maximum impact.
Implement Decisions
Users put choices into action. They monitor effects on the system. They adapt as necessary.
Effective Utilization of Interrelationship Digraphs
- Train Users
Educate participants. Teach them how to use the tool. Ensure correct application.
- Gather Diverse Perspectives
Collect input broadly. Involve stakeholders. Enhance the diagram's richness.
- Keep It Dynamic
Allow for updates. Respond to new information. Maintain relevance.
- Use Complementary Tools
Pair with other techniques. Enhance analysis. Strengthen decision-making.
- Review Periodically
Assess the digraph regularly. Update as situations evolve. Reflect continuous learning.
An interrelationship digraph serves as a powerful tool. It aids understanding and decision-making. It accommodates complexity in thoughtful ways. Users address root causes effectively. They make informed, impactful decisions. This tool enhances both strategic thinking and day-to-day management.